在人工智能与机器学习领域，线性回归是最基础、最核心的算法之一，它不仅是理解更复杂模型的基石，也是许多实际应用的起点。本文旨在系统梳理线性回归，特别是多元线性回归的基本概念、最优解求解方法，并结合有监督机器学习的工作流程，通过Jupyter Notebook的实践视角，为人工智能基础软件开发提供清晰的指引。

一、基本概念：什么是有监督机器学习与线性回归

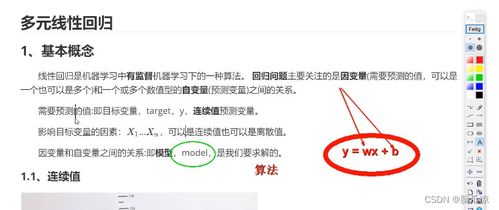
有监督机器学习是指模型从已标注的训练数据（即包含输入特征和对应输出标签的数据集）中学习规律，并用于对新数据进行预测。线性回归正是一种典型的有监督学习算法。其核心思想是：假设目标变量（因变量）与一个或多个特征变量（自变量）之间存在线性关系，并试图找到一个线性方程来最佳地拟合已知数据点。

简单线性回归：涉及一个自变量（特征）和一个因变量（目标），形式为 \( y = w1 x + b \)，其中 \( w1 \) 是权重（斜率），\( b \) 是偏置（截距）。

多元线性回归：这是本文的重点。当结果受到多个因素影响时，我们使用多元线性回归，其方程扩展为：

\[ y = w1 x1 + w2 x2 + ... + wn xn + b \]

其中，\( y \) 是预测值，\( x1, x2, ..., xn \) 是n个特征，\( w1, w2, ..., wn \) 是对应的权重（模型参数），\( b \) 是全局偏置。模型的目标是学习到一组最佳的 \( w \) 和 \( b \)。

二、核心目标：寻找最优解

“最优解”指的是能够使模型的预测值与真实值之间误差最小的那组参数。在线性回归中，我们通常使用最小二乘法作为衡量误差的标准，即最小化所有数据点上预测值与真实值之差的平方和，这个和被称为损失函数（或成本函数）。对于多元线性回归，损失函数 \( J \) 表示为：

\[ J(w, b) = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 \]

其中，\( m \) 是样本数量，\( \hat{y}^{(i)} \) 是第 \( i \) 个样本的预测值，\( y^{(i)} \) 是其真实值。

求解这个最优解主要有两种方法：

1. 解析解（正规方程）：通过数学公式直接计算参数。对于多元线性回归，公式为 \( \theta = (X^T X)^{-1} X^T y \)，其中 \( \theta \) 是包含所有权重和偏置的参数向量。这种方法在特征数量不多时计算高效，但特征维度很高或矩阵不可逆时可能不适用。
2. 数值优化解（梯度下降）：这是一种迭代方法。通过计算损失函数关于每个参数的梯度（导数），然后沿梯度反方向（即下降最快的方向）更新参数，逐步逼近最小值点。这是机器学习中最常用、最核心的优化算法，能够处理大规模数据集和复杂模型。

三、实践工具：Jupyter Notebook在人工智能基础软件开发中的角色

Jupyter Notebook是一个开源的Web应用程序，允许我们创建和共享包含实时代码、可视化、方程和叙述性文本的文档。它在人工智能基础学习和软件开发中不可或缺：

• 交互式探索：可以逐行或分块运行代码（如Python），立即看到结果，非常适合数据加载、预处理、模型训练和可视化的每一步探索。
• 可视化呈现：可以直接内嵌绘制损失函数下降曲线、数据分布散点图、回归拟合线等，直观理解模型行为和性能。
• 文档与报告：将代码、运行结果、数学公式（使用LaTeX）和文字说明结合在一个笔记本中，形成结构清晰的工作笔记或项目报告，便于知识沉淀和团队协作。
• 原型快速开发：在构建正式软件或系统前，可在Notebook中快速验证想法、测试算法和调整参数。

四、工作笔记与开发流程示例

在“人工智能工作笔记0040”中，一个典型的多元线性回归项目可能包含以下步骤：

1. 环境设置与数据导入：在Jupyter Notebook中导入必要的库（如NumPy, Pandas, Matplotlib, Scikit-learn）。
2. 数据理解与预处理：加载数据集，使用Pandas进行探索性分析；处理缺失值；对分类特征进行编码（如独热编码）；必要时进行特征缩放（如标准化），以加速梯度下降收敛。
3. 模型构建与训练：

• 从零实现：使用NumPy定义模型函数、损失函数和梯度下降算法，手动训练模型，深入理解原理。

• 使用框架：调用Scikit-learn的LinearRegression或SGDRegressor，快速构建和训练模型。

1. 评估与优化：在测试集上评估模型性能，使用指标如均方误差（MSE）、决定系数（R²）。分析结果，可能需要返回进行特征工程或调整正则化（如引入岭回归或Lasso以防止过拟合）。
2. 结果可视化与解释：绘制特征与预测值的关系图；对于高维模型，可绘制学习曲线或关键特征的权重条形图，以解释模型。
3. 与笔记：记录本次实验的关键发现、遇到的问题及解决方案、参数设置和最终模型性能。这为后续的模型迭代或更复杂的项目（如逻辑回归、神经网络）奠定了基础。

结论

线性回归，尤其是多元线性回归，为我们提供了一把打开有监督机器学习大门的钥匙。理解其基本概念、掌握求解最优解的数学原理和优化方法，是构建更复杂AI模型的基石。而Jupyter Notebook作为强大的交互式工具，极大地促进了从理论到实践的转化，使得学习、实验和软件开发过程更加高效和直观。在人工智能基础软件开发的旅程中，扎实掌握这些基础组件，并养成撰写清晰工作笔记的习惯，将为后续的深入探索奠定坚实的基础。